整列法(Sort)は,アルゴリズムの中でも最も基本的なものので,多くの研究がされ色々な整列法が開発されています。ここではその中でも最も初等的なものの一つである頻度整列法を紹介します。この方法は,「Basic 入門 プログラム例「ファイル処理の基本(成績処理プログラムを例にして)」で使ったものです。 アルゴリズムは使う状況によって最適な方法は違うのが常ですが,整列法もその例外ではありません。ですから,状況を判断して適切な方法を選択する必要があります。頻度整列法は初等的なもので,プログラムも簡単に作成でき,しかも高速に実行されます。頻度整列法はすべての状況で使えるとは限りませんが,状況によっては良い方法の一つです。
頻度整列法が都合よく働く状況は, データが比較的少数の離散的数値をとる ことが分かっている場合です。 例えば,1000人の学生の成績の順位をつけるような場合です。ここで成績は例えば,500点満点で小数点以下の点数がないとします。 そこで,以下この状況で考えましょう。即ち,1000人の学生が5科目の試験をしたとして,その合計点が分かっているとします。このとき,各学生が全体で何位であったかを求めるものとします。 学生に1から1000までの番号を付けて考えます。i番目の学生の点数を配列変数 Ten(i) で表します。またそのi番目学生の順位を Jun(i) と表します。 最初に Ten(i) の値が与えられていて,Jun(i) を求めるのが目標です。
頻度整列法はまず,頻度表を作り,その表から順位を計算する方法です。その方法は3段階に分けられます。各段階は極めて簡単なものです。
各段階を説明しましょう。 1.頻度表を作る。 頻度表は何点の学生が何人いるかの表です。 簡単のため,学生数10人とし,10点満点の例を挙げます。 Ten(1)= 2 Ten(2)= 1 Ten(3)= 3 Ten(4)= 7 Ten(5)= 2 Ten(6)= 5 Ten(7)= 0 Ten(8)= 4 Ten(9)= 2 Ten(10)= 3 この場合,頻度表は次のようになります。
頻度表 この頻度表の作り方は,簡単です。Ten(1)からTen(10)までその点に従って,各点のところに●を加えて行けばよいわけです。まず,この頻度表を配列変数 F(i) で表すことにします。これを計算するプログラムは For i=1 to 10 F(Ten(i))=F(Ten(i)) + 1 Next i となります。1000人の場合も形は全く同じです。配列変数の値に更に配列変数を入れて計算すればよいことが注意点です。 2.累積頻度表を作る。 頻度表は何点の人が何人という表でしたが,累積頻度表は何点以上の人が何人という表です。(今の場合高得点の人から順位を付けるので,何点以上になります。もし,点が少ない方から順位を付ける場合は,何点以下の人が何人という表を作ります。) この場合,累積頻度表は次のようになります。
累積頻度表 ●は頻度表でのものです,●はより多く点を取った人(右側にある●の個数)を表します。 この表の作り方も簡単です。頻度表で右にある点を順次加えれば良いわけです。右側からこの表を作っていくと,順次右側が累積頻度になっています。ですから,表の作り方は右隣を加えれば良いだけです。 この累積頻度表も頻度表を変更して作りますので,F(i) を累積頻度表を表すものに変更します。この変更をするプログラムは For i=10 to 1 Step -1 F(i)=F(i) + F(i+1) Next i となります。右端から始めますが,その場合 F(11) となり,元の配列から飛び出しますので,一つだけ余分に配列を用意します。 このプログラムを実行すると,頻度表 F(i) が累積頻度表 F(i) になります。 3.順位を決定する。 上の累積頻度表を参照して順位を決定します。 Ten(1) は点数が 2 点ですから,2のところの累積頻度表を見ます。この例では8になっています。この意味は,2点以上の点を取った人が8人ということですが,今の場合2点の人が3人います。 同じ点の人は同じ順位する必要がありますので,2点の人は6位とします。この6は実は3の累積頻度に1を加えたものになっています。 つまり,2点の人の順位は3点以上の人の次に来るわけですから,3の累積頻度5に1を加えて6を得ます。 同様に,k点の人の順位は,k+1点以上の人の数に1を加えて得られます。 このようにして, Jun(1)= 6 Jun(2)= 9 Jun(3)= 4 Jun(4)= 1 Jun(5)= 6 Jun(6)= 2 Jun(7)= 10 Jun(8)= 3 Jun(9)= 6 Jun(10)= 4 が得られます。プログラムは For i=1 to 10 Jun(i)=F(Ten(i)+1)+1 Next i となります。この場合も1つだけ余計に Jun(11) を確保しておく必要があります。 以上のプログラムをまとめると, For i=1 to 10 F(Ten(i))=F(Ten(i)) + 1 Next i For i=10 to 1 Step -1 F(i)=F(i) + F(i+1) Next i For i=1 to 10 Jun(i)=F(Ten(i)+1)+1 Next i となり,簡単ですね。 これで,データD(i) の人の順位 J(i) を決定できましたが,点数を出すだけでなく,点数順に並べる必要があるかもしれません。実際, 整列は実際のデータを並べ替えるものです。 上の方法ではまだ並べ替えているわけではありません。しかし,実は殆んど並べ替えは終わっていると考えても良いのです。 実際,Jun(i) を使うと,実際の並べ替えが次のように行われます。実際のデータを(1),(2),(3),...(10)と表します。まず,10個の箱を用意し,それに番号を付けます。
まず,Jun(1)は6ですから,(1)を6に入れます。次にJun(2)=9 ですから,(2)を9に入れます。同様にして,順に,Jun(3),Jun(4) を調べ(3),(4)を4,1に入れます。Jun(5)=6 ですが,6には既に(1)が入っているので開いている右隣7に入れます。以下同様に既に埋まっている場合は,順次右隣に入れることにすると,整列が終わります。このようにして,
が得られます。 この並べ代えは,上の表を配列変数S(i)で表すことで実現されたと考えられます。このS(i) の計算のプログラムは 上の操作をプログラミングすることで得られます。空の場合は S(i)=0 で表します。 For i=1 to 10
j = 0
While (S(Jun(i)+j)>0)
j = j + 1
Wend
S(Jun(i)+j)=i
Next i
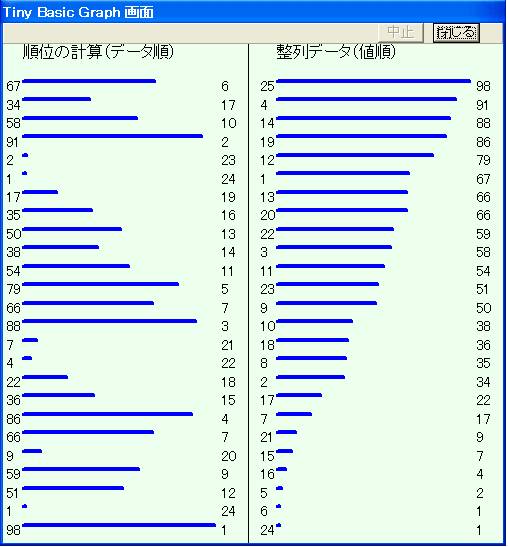
上の While 文は各データに対して実行されますが,同じ値のデータが沢山あると,この部分の実行が遅くになります。各Jun(i) に対して,j をどれ位取ったかを覚えておけば,これを防げます。そこで,配列変数ST(1) ~ST(10) を使うと,上の部分は For i=1 to 10 S(Jun(i)+ST(Jun(j))=i ST(Jun(i))= ST(Jun(i)+1 Next i と改良できます。 このアルゴリズム使った例のプログラムFre-sort.tbtはここにあります。 以下はその実行結果です。この例では,25個のデータ数,100点満点としています。左のグラフはデータ番号順に並んだもので,左に得点D(i),右に順位Jun(i)を表示しています。 右のグラフは,それを得点順に並べ替えたもので,左はデータ番号 i 右はその得点D(i)を表示しています。
頻度法の計算量はデータ数に比例して増えていきます。Jun(i) までの計算なら,データ数の3倍程度の繰り返し計算回数, S(i) までなら,5倍程度です。これは大変効率的な計算回数で,かなりのデータ数でも配列変数が確保できれば高速に可能です。 プログラム自体も簡単ですので,データが比較的少数の離散的数値をとる場合は,整列法として頻度法も現実的方法として考慮する対象の一つでしょう。 |