ハノイの塔は1883年にフランスのE.Lucas(リュカ)が考案したゲームと言われています。著書『数学遊戯』の中にあるそうです。 これは次のようなゲームです。
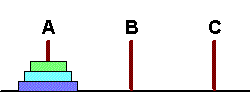
例 3枚の円盤の場合(n=3) 台の上に3本の棒A,B,Cが固定されていて,棒Aにn枚の円盤が棒を通して重ねられています。円盤は下へいくほど半径が大きくなっています。 このとき,次の規則に従って,円盤をAからBに移動してください。
このゲームは元々手で実際にやるものですし,実際に玩具としてこのようなものがあるそうです。しかしここではこれをプログラミングの問題,即ち,解く手順をコンピュータを使って求める問題としましょう。 プログラミングの問題としてはこのハノイの塔は再帰を使う典型例として有名なものです。 上の図にある3枚の円盤の場合を,実際に解くことは比較的簡単に思いつきます。しかし一般的に適用できるアルゴリズムを見つけるのは中々難しそうに見えます。実際,非再帰のプログラミング技法で解こうとすると大変難しい問題になります。 しかし,再帰を使うと以下のように驚くべき簡単なものとして実現できます。 Sub Hanoi(n,A$,B$,C$)
If n>0 then
Call Hanoi(n-1,A$,C$,B$)
Print n;"番の円盤を";A$;"から";B$;"へ移動"
Call Hanoi(n-1,C$,B$,A$)
End if
End Sub
説明をしましょう。アイデアは単純です。 円盤が2枚の場合を考えてみましょう。上から1,2と円盤に番号をつけます。この場合,AからBへの移動は次のようにして実現出来ます。
です。 さて一般の場合を考えます。その操作が出来たとして,その操作を Hanoi(n,A$,B$,C$) と表します。これはn枚の円盤をA$からB$にC$を補助的に使って移動するという操作です。 一般の場合,1からn-1の円盤を1纏まりとして考えて,それを1つの円盤と見ます。そうすると,2つの場合と同じ状況になります。このとき,(ア) に対応する操作はHanoi(n-1,A$,C$,B$)です。そして,(イ) はn番の円盤をAからBへ移動します。(ウ) は1纏まりとみた円盤をCからBへ移動しますから,Hanoi(n-1,C$,B$,A$)です。 これを再帰的プログラムにしたのが,上のHanoi です。これで終わりです!
「プログラムとは」の項で 良いプログラマは正しいプログラムを書くだけでなく, それが正しく動作することを分かりやすく証明する必要がある ということを書きました。その標語に従って上のプログラムが正しく動作すること証明しましょう。 いつもの通り,説明のため行番号を付けます。 01 Sub Hanoi(n,A$,B$,C$) 02 If n>0 then 03 Call Hanoi(n-1,A$,C$,B$) 04 Print n;"番の円盤を";A$;"から";B$;"へ移動" 05 Call Hanoi(n-1,C$,B$,A$) 06 End if 07 End Sub ここでHanoi(n,A$,B$,C$) という操作の意味を正確にしておく必要があります。
証明は数学的帰納法を使うのが適当です。
ハノイの塔の解法プログラム Hanoi での移動の回数を計算してみましょう。移動の回数を H(n) と表します。 Hanoi(n,A$,B$,C$)は3,4,5行で移動を出力しますが,3行は H(n-1) 回の移動,4行は 1回の移動, 5行はH(n-1)回の移動を出力します。従って, H(1)=1, n >1 のとき,H(n)=H(n-1)+1+H(n-1)=2*H(n-1)+1 となります。この漸化式は, H(1)=1, n>1 のとき, (H(n)+1)=2*(H(n-1)+1) と書けますから,H(n)+1 = 2n です。故に, H(n)=2n-1 となります。 この数値はかなり大きなものです。例えば,H(10)=1023ですし,H(40)=1099511627775となります。
プログラム Hanoi でハノイの塔の問題の解が得られることは分かりました。しかしその解法は n が大きくなるにつれて膨大な移動回数になります。 もっと良い方法は無いのでしょうか。しかし,実は ハノイの塔の解法は Hanoi が使ったアルゴリズムが最良 なのです。次にその証明をしてみましょう。 最良の移動法を与えるアルゴリズムをHanoiBest(n) という名前を付けましょう。これはn枚の円盤についてのハノイの塔の最良アルゴリズムを与えるものとします。このアルゴリズムを使って実際にハノイの塔を考えて見ます。 どのようなアルゴリズムを使っても,n番目の円盤をAからBへ移動しなくてはなりません。このとき,Bの棒には,n 以下の番号の円盤はあってはいけません。従って,このとき,1~n-1番目までの円盤は C にないといけません。従って,この時点で,HanoiBest(n) の中には HanoiBest(n-1) が少なくとも一回含まれないといけません。更に,n番目の円盤をAからBへ移動した後,Cにある1~n-1の円盤を戻さないといけませんから,その後で少なくとも,もう一回HanoiBest(n-1)を含む必要があります。従って, HanoiBest(n) の中にはHanoiBest(n-1)を2回と1回の移動が含まれます。 そこで,HanoiBest(n) が出力する移動の回数を HB(n) と表すと,今のことから, HB(n) ≧2*HB(n-1) + 1 が得られます。明らかに, HB(1)=1 ですから,Hanoi で使った H(n) と比較すると,上の式ですべて等号が成立するのが H(n) ですから, HB(n) ≧ H(n) が得られます。従って,HanoiBest が最良であると言うことから,HB(n)=H(n) となります。即ち, Hanoi が出力する移動の回数が最良 と言うことになります。 最後に,Hanoi をTiny Basic での実行するための補足をします。 Tiny Basic のプログラムとして実行する場合は,Hanoi を call して下さい。例えば次がn=5 の場合の完全なプログラムです。 Call Hanoi(5,"A","B","C")
End
Sub Hanoi(n,A$,B$,C$)
If n>0 then
Call Hanoi(n-1,A$,C$,B$)
Print n;"番の円盤を";A$;"から";B$;"へ移動"
Call Hanoi(n-1,C$,B$,A$)
End if
End Sub
|