整列法（Sort）は，アルゴリズムの中でも最も基本的なものので，多くの研究がされ色々な整列法が開発されています。ここではその中でも 最も代表的な整列法であるクイック整列法を紹介します。 クイック整列法はクイックソートと英語のままで呼ばれることが多いので，以下では，クイックソートと言うことにします。

　この整列法は1960年 C.A.R. Hoareによって発明された整列法です。平均的には最も高速な方法ということで，クイックソートと呼ばれ，現在最もよく使われる整列法です。

　 選択整列法の場合と同じ状況を考えましょう。すなわち，ランダムに与えられた，文字列を辞書順に整列することを考えます。

　簡単にためのアルファベットからなる10個文字列が与えられ，それを辞書順の整列することを考えます。（住所録で名前順に整列する場合も同様です。）

　実際は1000個の文字列でも全く同様に動作します。

　与えられた文字列が配列変数で D$(1), D$(2), ..., D$(10) と与えられたとします。この中身を入れ替えて，辞書順に D$(1), D$(2), ..., D$(10) を作ります。例えば，

ということです。

　 クイックソートは，まず，全体データを適当に処理して，次のようにします。

　まず適当に，あるデータＰを取ります。このデータが最終的にどこに来るか決め，それを基点として，左右に２つに分けて，右側のデータはすべて，Ｐ以上，左側のデータはすべてＰ以下であるように する。つまり，

Ｐの左側のデータ≦Ｐ≦Ｐの右側のデータ

であるようにします。

　この処理を Partition と呼びましょう。この処理が一般的に得られたとすると，クイックソートQSort は左データ，右データについて同様なことを行うことで全体を整列するものです。

　この Partition を認めるとQSort は再帰的表現を使って次のように簡単に書けます。（説明のため行番号を付けています。）

01 Sub QSort(left,right)
02    if left < right then
03       p = Partition(left, right)
04       Call QSort(p+1, right)
05       Call QSort(left, p-1)
06    end if
07 End Sub

ここで，QSort(left,right)は D$(left) とD$(right) の間のデータをクイックソートで整列することを示します。

　１行目は，Sub 宣言です。 QSort(left,right) と宣言しています。

　２行目は，終了判定です。 left = right になったら，データが一個ですから，終わりです。それ以外は以下の処理を行います。

　３行目で，Partition(left,right) を行います。このPartition(left,right)はleft とright の間のデータを分割するということ示しています。 p=Partition(left,right) はその結果Ｐの位置を返しています。

　４行目では，Partition の結果，右側となったデータを更に QSort で整列するという再起呼び出しを行っています。

　５行目では，Partition の結果，左側となったデータを更に QSort で整列するという再起呼び出しを行っています。

　このように，QSort の本質的部分は　Partition と言えます。そこで次にこのPartition について説明しましょう。

　この操作Partitionは例えば次のようにすると実現されます。

1. 適当にデータＰを取ります。
2. Ｐをとりあえず，左端に移します。
3. Ｐの右隣から順次，データを調べて，Ｐ以下のデータがあったら，それを，左データの組に入れ，Ｐ以上のデータがあったら，右データの組に入れます。
4. 最後にＰを左データの組と右データの組の間にＰを入れます。

　ここで，３の処理をもう少し具体的に表してみます。

• まず最初は左データの組は空であるとします。
• 左データの組に入るデータがあったら，Ｐの隣から順次埋めていきます。
• その際，左データの組の個数を数えながら操作を行って行きます。
• そうすると，左データが現れたとき，埋める位置がその個数から分かります。
• 最後まで調べ終わったとき，左データの組に入っていないものは，右データの組に入ります。
• そこで，その境目（それは右データの個数から分かります）にＰを移動して操作が終わります。

以上の操作をプログラムで表してみると次のようになります。（説明のため行番号を付けています。）

01 Function Partition(left,right)
02    Call Change(left, Int((left+right)/2))
03    last = left
04    for i= left + 1 to right
05       if (D$(i) < D$(left)) then 
06          last = last + 1
07          Call Change(last,i)
08       end if
09    next i
10    Call Change(left,last)
11    Partition = last
12 End Function　

ここで，使われている Change(,a,b) は D$(a) と D$(b) を交換する処理を表しています。

１行目は関数宣言です。この操作を Partition(left,right) という関数で表します。これはleftから right の間にあるデータについてその操作を行うことにして，データＰの位置を関数の値として，返します。

２行目はＰを取っています。原理的にはどれでも良いですが，ここではＰとして中央にあるデータを取り，それを左端に置きます。

３行目の last はＰが最終的に置かれる位置を求めるための変数です。last - left がＰの左データの個数を表します。最初は last - left = 0 です。

４行目から９行目までが，データをＰの左右に分ける部分です。

５行目で，もしD$(i) < D$(left)なら， D$(i) はＰの左にあるデータです。そこでこの場合，Ｐの左に置きますから，Ｐの最終的位置は１だけ右に移動します。これが６行目の， last = last + 1です。７行目の Change(last,i) はそのデータをlast の位置に入れ替えています。左端に取りあえず置いたＰ以外，last の位置より左にあるデータがＰの左データになっています。

４行から９行が終わった時点で，left+1から last の位置にあるデータがＰの左データです。ですから，１０行で左端に取りあえず置いたＰと last の位置にある データを入れ替えると，操作が終わることになります。１１行ではlastを関数値として返しています。

　この操作を実際の簡単な場合に実行してみましょう。見易さのためデータは数とします。

　とデータが並んでいたとします。上段は i を表し，下段は　D$(i) を表しています。

このデータに対して，p=Partition(1,10) を実行してみましょう。

１．Ｐの決定：中央値としてＰを取ります。D$(5)="６"がＰです。

２．Ｐを左端に移動：1と5を入れ替えます。

last=1

３．i=2から処理を始めます。黄色が左データ

last=2

last=3

last=3：変わらない

last=4："３"と"７"の交換

last=4：変わらない

last=4：変わらない

last=4：変わらない

last=5："４"と"７"の交換

last=6："１"と"９"の交換

４．最後に1とlastの交換（"６"と"１"の交換）して操作の終わり。

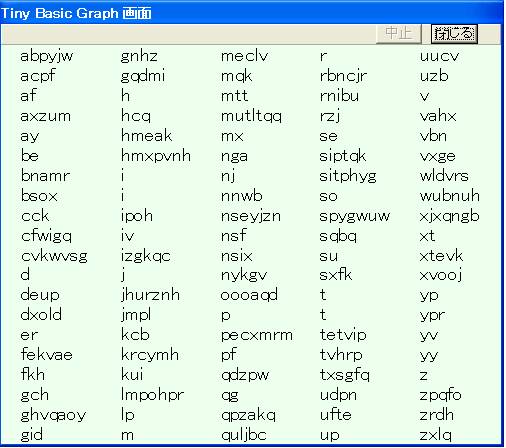
　このアルゴリズム使った例のプログラムQ-sort.tbtがここにあります。 以下はその実行結果です（多少変更しています）。ここでは 100個の文字列をクイックソートで整列しています。

　クイックソートの計算量はデータの並び方によって違います。データがランダムに並んでいたとすると，

比較回数は大体 2NlogNで，交換回数はその半分程度です。選択整列法に比べて比較回数が少ないことが目立ちます。大きなデータ数の場合この違いは歴然です。

　実際，私の手元のTiny Basic での実験によれば，5000件のデータでも数秒で，整列可能です。また上の例プログラムQ-sort.tbt でも速すぎて，動きを確認できないので，わざと遅延させています。