整列法（Sort）は，アルゴリズムの中でも最も基本的なものので，多くの研究がされ色々な整列法が開発されています。ここではその中でも基本的なものの一つである選択整列法を紹介します。

　選択整列法は比較的簡単な方法ですが，頻度整列法より一般的で，提供範囲も広く，比較的高速です。余り大量ではないデータを簡単に整列するのに適しています。

　 ランダムに与えられた，文字列を辞書順に整列することを考えましょう。文字列のとりうる場合はかなり数になります。例えば，高々１０文字のアルファベットから出来る文字列を考えると，全部で

26+26²+26³+ ...+26¹⁰ = 146813779479510

種類あり，頻度法で行うのは無理です。選択整列法はこの場合でも十分動作します。選択整列法は

データの個数が余り多くなければ

その，とり得る場合の数自身は多くても十分動作します。

　簡単にためのアルファベットからなる10個文字列が与えられ，それを辞書順の整列することを考えます。（住所録で名前順に整列する場合も同様です。）

　実際は1000個の文字列でも全く同様に動作します。

　与えられた文字列が配列変数で D$(1), D$(2), ..., D$(10) と与えられたとします。この中身を入れ替えて，辞書順に D$(1), D$(2), ..., D$(10) を作ります。例えば，

ということです。

　選択整列法は，まず， 一番先頭になるべきものを探し，それを１番に先頭に入れ，次に残りのもので一番先頭になるべきものを探し，それを次の先頭に入れるという方法です。全く単純な方法です。

　文字列比較では，前のものが，小さいと解釈します。例えば

"abc" < "acb"

です（Tiny Basic では　Ver. 1.075 以降が文字列比較可能）。ですから，以下では，辞書順で先頭のものを最小なものと言うことにします。

　少数のデータに対して，この操作を手で行うとすると全く簡単なことですが，それをプログラムにするとすると，少し考える必要があります。

　選択整列法はでは，次の２つの処理が本質的です。

1. 最小データを見つける。
2. 最小データを一番前に移動する。

各段階を説明しましょう。

１．最小データを見つける。

　D$(1) から D$(10) まで，順次比較しその最小値を見つけます。

方法は，まず，最小値の候補をD$(1)とします。これと D$(2)を比較します。D$(1)<D$(2) ですから，候補はD$(1)のままです。次に，D$(3) と比較します。この場合は，D$(1) > D$(3) ですから，最小値の候補をD$(1) から， D$(3) に代えます。次に D$(3) と D$(4) を比較します。この場合， D$(3) < D$(4) ですから，候補は D$(3) のままです。同様に，D$(5), D$(6), D$(7), D$(8), D$(9), D$(10) と比較して，も D$(3) が小さいので，D$(3) が最小値であることが分かります。

この処理をプログラムで表すと，最小値の候補を　mini に入れておくとして，

mini = 1
For j = i+1 to 10
   if D$(mini) > D$(j) then mini = j
Next j 　

となります。今の場合，上の操作が終わると， mini = 3 になっています。

２．最小データを一番前に移動する。

　最小データ D$(3) を一番前のデータ D$(1) と入れ替えます。

この処理をプログラムで表すと，

TD$ = D$(mini)
D$(mini) = D$(1)
D$(1) = TD$

となります。

１，２の処理が終わると，D$(1) が最小値になっています。そこで同様の操作を D$(2) ～ D$(10) について行います。

D$(2) ～ D$(10) までの間の最小値は D$(10)="cbyb" です。そこでそれを D$(2) と入れ替えます。

以下同様に，D$(3) ～ D$(10)を行い，これを繰り返します。

　以上の操作のプログラムは以下の通りです。

For i=1 to 10
   mini = i
   For j= i+1 to 10
      if D$(mini) > D$(j) then mini = j
   Next i
   if min > i then
      TD$ = D$(mini)
      D$(mini) = D$(1)
      D$(1) = TD$
   end if
Next i

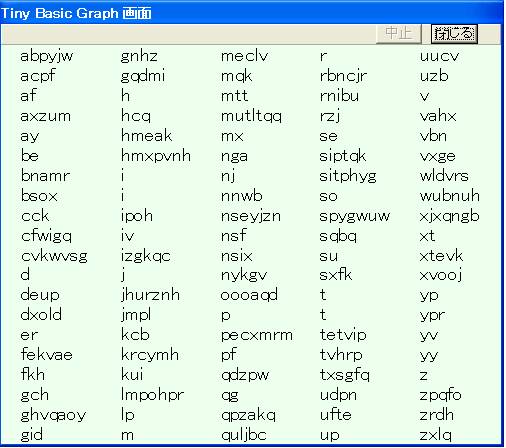
　このアルゴリズム使った例のプログラムSel-sort.tbtはここにあります。 以下はその実行結果です（多少変更しています）。ここでは 100個の文字列を選択整列法で整列しています。

　選択整列法の計算量はデータ数を N とすると，比較回数は大体 N²/2，データの交換回数はデータ の散らばり具合によって違いますが，最大でＮ-1に なります。

　比較回数はN²/2と少なくはありませんが，交換回数は少なく，プログラム自体も簡単ですので，データ数が 余り多くない場合は，選択整列法は良い整列法と言えます。

　実際，私の手元のTiny Basic での実験によれば，5000件のデータでも1分程度で，整列可能です。