再帰的アルゴリズム

再帰的アルゴリズム

　再帰的（recursive）アルゴリズムはアルゴリズムでの基本的手法の一つです。ここではそれについて簡単に説明します。

　Recursive という言葉は帰納的と訳される場合もあります。帰納的関数と再帰的関数と言う場合，これらは本質的には同じです。しかし，inductive も帰納と訳されます。数学的帰納法の帰納は inductive の方です。

　一般に再帰と帰納は，少しニュアンスの違いがあります。

再帰的とは

　あるものが定義されている場合，

その定義の中に，更にその定義されるべきものが，簡単化されて，含まれているとき，

それは「再帰的である」と言われます。循環論法に似ていますが，少し違います。再帰的はその部分に含まれるものが全く同じものではなくて，簡単になったもので，最終的終了条件が明示されているものです。

再帰的定義の例

　よく挙げられる例として，階乗関数があります。階乗関数ｎ！は

ｎ！＝１・２・３・・・ｎ

で定義されるものです。この定義はこれでよいのですが，よく考えてみると，・・・と言う部分を含んでいて，この・・・の意味が明確とは言えません。そこで，もう少し明確な定義として，

０！＝１，

ｎ＞０　のとき，　ｎ！＝（ｎ－１）！・ｎ

とすることも出来ます。

　ここで，ｎ！の定義式の右辺に，（ｎ－１）！という階乗関数の式が表れてることに注意して下さい。階乗関数が表れていますが，しかし，この式は左辺の階乗関数ｎ！よりも簡単なものです。そして，ｎ＝０の場合，０！＝１であると定められています。

　この定義を使って，実際に３！を計算してみると，次のようになります。

３＞０だから，　３！＝２！＊３　

ここで，２！を計算する。

２＞０だから，２！＝１！＊２

ここで１！を計算する。

１＞０だから，１！＝０！＊１

ここで０！＝１である。これを使って，上の計算を逆にたどる。

１！＝０！＊１＝１＊１＝１

２！＝１！＊２＝１＊２＝２

３！＝２！＊３＝２＊３＝６

このようにして３！が計算されます。

　このような定義の仕方を再帰的定義と言います。

この階乗関数を Basic プログラムとして実現してみると，（Tiny Basic には階乗関数 Factorial が内蔵されていますから，実際にこのようなプログラムを書く必要はありませんが。）

Function Kaijyou(n)
   If n = 0 then
      Kaijyou = 1
   Else
      Kaijyou = Kaijyou(n-1)*n
   End if   
End Function

となります。しかし，実は階乗関数は，再帰を使わなくても，次のように実現することが出来ます。

Function Kaijyou(n)
   F = 1
   For i = 1 to n
      F = F * i
   Next i
   Kaijyou = F
End Function

　このように再帰的プログラムの多くは再帰を使わないものに書き直すことが出来ます。

再帰的定義の別の例

　再帰的に定義される別の例を挙げてみましょう。

　それは漸化式で定義される数列です。一般の場合も同様ですが，最も簡単な有名な例として，フィボナッチの数列を紹介します。フィボナッチの数列 F(n) は次のように定義されるものです。

F(1)=1， F(2)=1， n>2 のとき F(n)=F(n-1)+F(n-2)

これによると例えば，F(3)=2, F(4)=3, F(5)=5, F(6)=8, ... となります。このフィボナッチ数はかなり急速に大きくなる数で，例えば

F(50)=12586269025

となります。

　このフィボナッチの数列の計算の再帰を使ったプログラム１を挙げます。

プログラム１
Function Fib(n)
   If ((n=1) or (n=2)) then
      Fib= 1
   Else
      Fib = Fib(n-1)+Fib(n-2)
   End if
End function

　このプログラムは定義そのままで，分かりやすいですね。このプログラムも再帰を使わないで，次のように書くことが出来ます。

プログラム２
Function Fib(n)
   a = 1
   b = 1
   For i=3 to n
      c = a + b
      b = a
      a = c
   Next i
   Fib = a
End Function

　これはプログラム１よりも，少し分かりにくいですが，それほど複雑ではありません。

　ここで，プログラム１とプログラム２の計算の効率を比較してみましょう。

　プログラム２の評価は簡単です。 For Next 文の中が n-2 回実行されます。その前後と合わせると大体 n 回，For Next 文の中が実行される程度の計算です。ですから，１回の繰り返しで３つの計算をするとして，n=50 のときの計算回数は150回程度です。

　これに対して，プログラム１の評価は少し複雑です。

　すぐに分からないので，Fib(n) を計算するときに行う計算回数を仮に，NF(n) と表したとします。NF(1)やNF(2)は If 文の中を１回実行するだけですから，ともに1であるとします。3以上のnに対しては，If のElse の部分が実行されます。ここで，Fib(n-1) の計算と Fib(n-2) の計算はそれぞれ独立に計算されますから，それにかかる計算回数はそれぞれ，NF(n-1)，NF(n-2) です。そしてこの場合， NF(n) の計算はそれを併せたものですから，NF(n)=NF(n-1)+NF(n-2) が大体成立します。 Fib(n) を呼ぶ時の手間を考えれば実際はそれ以上になります。

　以上のことを良く見ると， NF(n) は大体 Fib(n) つまり，フィボナッチの数列と同じ程度，もしくはそれ以上の計算回数が必要になることが分かります。

　さてここで例えば，n=50 の時を考えてみるとプログラム１は値を求めるのにフィボナッチ数 Fib(50)=12586269025回以上の計算を必要とします。プログラム２の計算回数 150 との比較は一目瞭然です。

　Tiny Basic では平均して，私の機械で１秒間少なくとも10万回程度の計算が可能です。そこで，１秒間に10万回行うとします。プログラム２で Fib(50) を計算するのは一瞬です。これに対してプログラム１では，87日掛かる計算になります。

　実のところ，

フィボナッチの数列の計算に

上のプログラム１ような再帰プログラムを使うのは

やってはいけないこと

として有名なものなのです。このような場合は非再帰プログラムを使うべきなのです。上の階乗関数の場合も，再帰を使う理由は実はありません。

再帰は使うべきか

　このように見てくると，再帰プログラムは効率の良くないプログラムと思うかもしれません。実はある意味ではその通りです。それでは使う必要のないものなのでしょうか？これも使わなくて良ければと言う前提に立てばその通りです。

　一般に次のことが言えます。

再帰プログラムは計算機に負荷をかけるプログラムである。
時によっては，膨大な負荷をかけることもある。
簡単に非再帰プログラムとして書けるものは再帰プログラムを使うべきではない。

　それでも，再帰プログラムが基本的であると言われるのは何故でしょうか。それは再帰プログラムが大きな力を秘めているからです。つまり

再帰プログラムでは簡単に書けるが，非再帰プログラムはかなり複雑なプログラムになってしまうようなものがある。

ということです。

　このような問題が意外とあるのです。再帰プログラム技法を，身につけたら，プログラミングを行う際，次のような視点で考えるのが良いかもしれません。

まずは，非再帰プログラムで問題を考えてみる。
難しいと判断した場合，再帰プログラムで考えてみる。

　再帰プログラムの例はこれから，Basic によるアルゴリズム入門の項で順次取り上げていきますので，ここでは再帰プログラムが有効な例を一つだけ挙げることにします。

再帰が有効な例

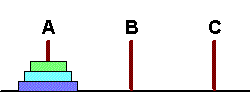
　ここでの例はハノイの塔です。ハノイの塔は次のようなゲームです。

　台の上に３本の棒A，B，Cが固定されていて，そのうちの一本に何枚かの円盤が棒を通して重ねられています。円盤は下へいくほど半径が大きくなっています。

　このとき，次の規則に従って，円盤をＡからBに移動してください。

一回に一枚の円盤しか動かしてはいけません。
移動の途中で円盤の大小を逆に積んではいけません。常に大きい方の円盤が下になるようにして下さい。
棒A，B，C以外のところに円盤を置いてはいけません。

　これを解く手順をプログラミングするのが問題です。一見して，上の図にある３の場合を，実際に解くことは比較的簡単に思いつきます。しかし一般的に適用できるアルゴリズムを見つけるのは中々難しそうに見えます。実際，非再帰のプログラミング技法で解こうとすると大変難しい問題になります。

　しかし，再帰を使うと以下のように，驚くべき簡単なものとして実現できます。

Sub  Hanoi(n,A$,B$,C$)
   If n>0 then
      Call Hanoi(n-1,A$,C$,B$)
      Print n;"番の円盤を";A$;"から";B$;"へ移動"
      Call Hanoi(n-1,C$,B$,A$)
   End if
End Sub

　ハノイの塔の詳しい説明は，別にしました。プログラムの背景「ハノイの塔」を参照して下さい。